Tim Olimpiade Matematika Kota Banjar: Fields of Math part 1

Fields of Mathematics

edited By:
Arip Nurahman
Indonesia University of Education

As noted above, the major disciplines within mathematics first arose out of the need to do calculations in commerce, to understand the relationships between numbers, to measure land, and to predict astronomical events. These four needs can be roughly related to the broad subdivision of mathematics into the study of quantity, structure, space, and change (i.e., arithmetic, algebra, geometry, and analysis). In addition to these main concerns, there are also subdivisions dedicated to exploring links from the heart of mathematics to other fields: to logic, to set theory (foundations), to the empirical mathematics of the various sciences (applied mathematics), and more recently to the rigorous study of uncertainty.

Quantity

The study of quantity starts with numbers, first the familiar natural numbers and integers ("whole numbers") and arithmetical operations on them, which are characterized in arithmetic. The deeper properties of integers are studied in number theory, whence such popular results as Fermat's last theorem. Number theory also holds two widely-considered unsolved problems: the twin prime conjecture and Goldbach's conjecture.

As the number system is further developed, the integers are recognized as a subset of the rational numbers ("fractions"). These, in turn, are contained within the real numbers, which are used to represent continuous quantities. Real numbers are generalized to complex numbers. These are the first steps of a hierarchy of numbers that goes on to include quarternions and octonions. Consideration of the natural numbers also leads to the transfinite numbers, which formalize the concept of counting to infinity. Another area of study is size, which leads to the cardinal numbers and then to another conception of infinity: the aleph numbers, which allow meaningful comparison of the size of infinitely large sets.

Natural Number

In mathematics, a natural number (also called counting number) can mean either an element of the set {1, 2, 3, ...} (the positive integers) or an element of the set {0, 1, 2, 3, ...} (the non-negative integers). The former is generally used in number theory, while the latter is preferred in mathematical logic, set theory, and computer science. A more formal definition will follow.

Natural numbers have two main purposes: they can be used for counting ("there are 3 apples on the table"), and they can be used for ordering ("this is the 3^rd largest city in the country").

Properties of the natural numbers related to divisibility, such as the distribution of prime numbers, are studied in number theory. Problems concerning counting, such as Ramsey theory, are studied in combinatorics.

The Integer

The integers (from the Latin integer, which means with untouched integrity, whole, entire) are the set of numbers consisting of the natural numbers including 0 (0, 1, 2, 3, ...) and their negatives (0, −1, −2, −3, ...). They are numbers that can be written without a fractional or decimal component, and fall within the set {... −2, −1, 0, 1, 2, ...}. For example, 65, 7, and −756 are integers; 1.6 and 1½ are not integers. In other terms, integers are the numbers one can count with items such as apples or fingers, and their negatives, including 0.

More formally, the integers are the only integral domain whose positive elements are well-ordered, and in which order is preserved by addition. Like the natural numbers, the integers form a countably infinite set. The set of all integers is often denoted by a boldface Z (or blackboard bold $\mathbb{Z}$ , Unicode U+2124 ℤ), which stands for Zahlen (German for numbers).^[1]

In algebraic number theory, these commonly understood integers, embedded in the field of rational numbers, are referred to as rational integers to distinguish them from the more broadly defined algebraic integers.

Rational Number

In mathematics, a rational number is a number which can be expressed as a ratio of two integers. Non-integer rational numbers (commonly called fractions) are usually written as the vulgar fraction 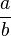$\frac{a}{b}$ , where b is not zero. a is called the numerator, and b the denominator.

Each rational number can be written in infinitely many forms, such as $\frac{3}{6} = \frac{2}{4} = \frac{1}{2}$ , but it is said to be in simplest form when a and b have no common divisors except 1 (i.e., they are coprime). Every non-zero rational number has exactly one simplest form of this type with a positive denominator. A fraction in this simplest form is said to be an irreducible fraction, or a fraction in reduced form.

The decimal expansion of a rational number is eventually periodic (in the case of a finite expansion the zeroes which implicitly follow it form the periodic part). The same is true for any other integral base above one, and is also true when rational numbers are considered to be p-adic numbers rather than real numbers. Conversely, if the expansion of a number for one base is periodic, it is periodic for all bases and the number is rational. A real number that is not a rational number is called an irrational number.

Real Number

In mathematics, the real numbers may be described informally as numbers with an infinite decimal representation, such as 2.4871773339.... The real numbers include the rational numbers, such as 42 and −23/129, and the irrational numbers, such as π and the square root of 2. They can also be visualized, or represented, as points along an infinitely long number line.

A rigorous definition of the real numbers was one of the most important developments of 19th century mathematics. Indeed, several equivalent definitions were developed. Popular approaches that are still used nowadays include

the real numbers as equivalence classes of Cauchy sequences of rational numbers,
the real numbers as Dedekind cuts, a more sophisticated version of "decimal representation", and
the real numbers as the unique complete Archimedean ordered field.

The name real numbers arose to distinguish them from what were then called imaginary numbers (and now complex numbers).

Complex Numbers

In mathematics, the complex numbers are an extension of the real numbers obtained by adjoining an imaginary unit, denoted i, which satisfies:^[1]

$i^2=-1.\,$

Every complex number can be written in the form a + bi, where a and b are real numbers called the real part and the imaginary part of the complex number, respectively.

Complex numbers are a field, and thus have addition, subtraction, multiplication, and division operations. These operations extend the corresponding operations on real numbers, although with a number of additional elegant and useful properties, e.g., negative real numbers can be obtained by squaring complex (imaginary) numbers.

Complex numbers were first discovered by the Italian mathematician Girolamo Cardano, who called them "fictitious", during his attempts to find solutions to cubic equations ^[2]. The solution of a general cubic equation may require intermediate calculations containing the square roots of negative numbers, even when the final solutions are real numbers, a situation known as casus irreducibilis. This ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, it is always possible to find solutions to polynomial equations of degree one or higher.

The rules for addition, subtraction, multiplication, and division of complex numbers were first developed by the Italian mathematician Rafael Bombelli. A more abstract formalism for the complex numbers was further developed by the Irish mathematician William Rowan Hamilton, who extended this abstraction to the theory of quaternions.

Complex numbers are used in many different fields including applications in engineering, electromagnetism, quantum physics, applied mathematics, and chaos theory. When the underlying field of numbers for a mathematical construct is the field of complex numbers, the name usually reflects that fact. Examples are complex analysis, complex matrix, complex polynomial and complex Lie algebra.