Applied mathematics considers the use of abstract mathematical tools in solving concrete problems in the
, and other areas. An important field in applied mathematics is
as a tool and allows the description, analysis, and prediction of phenomena where chance plays a role. Most experiments, surveys and observational studies require the informed use of statistics. (Many statisticians, however, do not consider themselves to be mathematicians, but rather part of an allied group.)
investigates computational methods for efficiently solving a broad range of mathematical problems that are typically too large for human numerical capacity; it includes the study of
or other sources of error in computation.
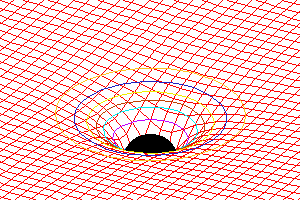 Mathematical physics
Mathematical physicsMathematical physics is the scientific discipline concerned with the interface of mathematics and physics. There is no real consensus about what does or does not constitute mathematical physics. A very typical definition is the one given by the Journal of Mathematical Physics: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and for the formulation of physical theories."[1]
This definition does, however, not cover the situation where results from physics are used to help prove facts in abstract mathematics which themselves have nothing particular to do with physics. This phenomenon has become increasingly important, with developments from string theory research breaking new ground in mathematics. Eric Zaslow coined the phrase physmatics to describe these developments[2], although other people would consider them as part of mathematical physics proper.
Important fields of research in mathematical physics include: functional analysis/quantum physics, geometry/general relativity and combinatorics/probability theory/statistical physics. More recently, string theory has managed to make contact with many major branches of mathematics including algebraic geometry, topology, and complex geometry.
Contents
 Mathematical fluid dynamics
Mathematical fluid dynamicsEdited By:
Arip Nurahman
Indonesia University of education
Sources from:
Wikipedia
Fluid mechanics is the study of how fluids move and the forces on them. (Fluids include liquids and gases.) Fluid mechanics can be divided into fluid statics, the study of fluids at rest, and fluid dynamics, the study of fluids in motion. It is a branch of continuum mechanics, a subject which models matter without using the information that it is made out of atoms. The study of fluid mechanics goes back at least to the days of ancient Greece, when Archimedes made a beginning on fluid statics. However, fluid mechanics, especially fluid dynamics, is an active field of research with many unsolved or partly solved problems. Fluid mechanics can be mathematically complex. Sometimes it can best be solved by numerical methods, typically using computers. A modern discipline, called Computational Fluid Dynamics (CFD), is devoted to this approach to solving fluid mechanics problems. Also taking advantage of the highly visual nature of fluid flow is Particle Image Velocimetry, an experimental method for visualizing and analyzing fluid flow. Fluid mechanics is that branch of physics which deals with the properties of fluid,namely liquid and gases,and their interaction with forces.
Contents
 Numerical analysis
Numerical analysisEdited By:
Arip Nurahman
Indonesia University of education
Sources from:
Wikipedia
Numerical analysis is the study of algorithms for the problems of continuous mathematics (as distinguished from discrete mathematics).
One of the earliest mathematical writings is the Babylonian tablet YBC 7289, which gives a sexagesimal numerical approximation of  , the length of the diagonal in a unit square.[1] Being able to compute the sides of a triangle (and hence, being able to compute square roots) is extremely important, for instance, in carpentry and construction.[2] In a rectangular wall section that is 2.40 meter by 3.75 meter, a diagonal beam has to be 4.45 meters long.[3]
, the length of the diagonal in a unit square.[1] Being able to compute the sides of a triangle (and hence, being able to compute square roots) is extremely important, for instance, in carpentry and construction.[2] In a rectangular wall section that is 2.40 meter by 3.75 meter, a diagonal beam has to be 4.45 meters long.[3]
Numerical analysis continues this long tradition of practical mathematical calculations. Much like the Babylonian approximation to  , modern numerical analysis does not seek exact answers, because exact answers are impossible to obtain in practice. Instead, much of numerical analysis is concerned with obtaining approximate solutions while maintaining reasonable bounds on errors.
, modern numerical analysis does not seek exact answers, because exact answers are impossible to obtain in practice. Instead, much of numerical analysis is concerned with obtaining approximate solutions while maintaining reasonable bounds on errors.
Numerical analysis naturally finds applications in all fields of engineering and the physical sciences, but in the 21st century, the life sciences and even the arts have adopted elements of scientific computations. Ordinary differential equations appear in the movement of heavenly bodies (planets, stars and galaxies); optimization occurs in portfolio management; numerical linear algebra is essential to quantitative psychology; stochastic differential equations and Markov chains are essential in simulating living cells for medicine and biology.
Before the advent of modern computers numerical methods often depended on hand interpolation in large printed tables. Nowadays (after mid 20th century) these tables have fallen into disuse, because computers can calculate the required functions. The interpolation algorithms nevertheless may be used as part of the software for solving differential equations and the like.
Contents
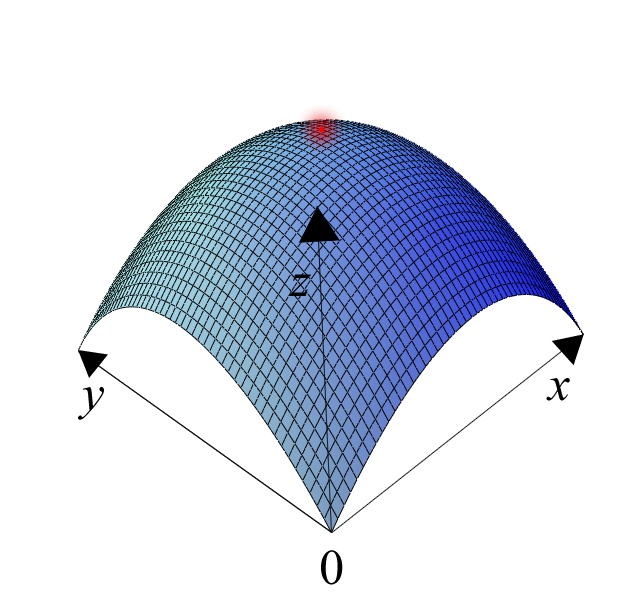 Optimization
OptimizationEdited By:
Arip Nurahman
Indonesia University of education
Sources from:
Wikipedia
In mathematics, the term optimization, or mathematical programming, refers to the study of problems in which one seeks to minimize or maximize a real function by systematically choosing the values of real or integer variables from within an allowed set.
Overview
An optimization problem can be represented in the following way
- Given: a function f : A
 R from some set A to the real numbers
R from some set A to the real numbers - Sought: an element x0 in A such that f(x0) ≤ f(x) for all x in A ("minimization") or such that f(x0) ≥ f(x) for all x in A ("maximization").
Such a formulation is called an optimization problem or a mathematical programming problem (a term not directly related to computer programming, but still in use for example in linear programming - see History below). Many real-world and theoretical problems may be modeled in this general framework. Problems formulated using this technique in the fields of physics and computer vision may refer to the technique as energy minimization, speaking of the value of the function f as representing the energy of the system being modeled.
Typically, A is some subset of the Euclidean space Rn, often specified by a set of constraints, equalities or inequalities that the members of A have to satisfy. The domain A of f is called the search space, while the elements of A are called candidate solutions or feasible solutions.
The function f is called an objective function, or cost function. A feasible solution that minimizes (or maximizes, if that is the goal) the objective function is called an optimal solution.
Generally, when the feasible region or the objective function of the problem does not present convexity, there may be several local minima and maxima, where a local minimum x* is defined as a point for which there exists some δ > 0 so that for all x such that

the expression

holds; that is to say, on some region around x* all of the function values are greater than or equal to the value at that point. Local maxima are defined similarly.
A large number of algorithms proposed for solving non-convex problems – including the majority of commercially available solvers – are not capable of making a distinction between local optimal solutions and rigorous optimal solutions, and will treat the former as actual solutions to the original problem. The branch of applied mathematics and numerical analysis that is concerned with the development of deterministic algorithms that are capable of guaranteeing convergence in finite time to the actual optimal solution of a non-convex problem is called global optimization.
History
The first optimization technique, which is known as steepest descent, goes back to Gauss. Historically, the first term to be introduced was linear programming, which was invented by George Dantzig in the 1940s. The term programming in this context does not refer to computer programming (although computers are nowadays used extensively to solve mathematical problems). Instead, the term comes from the use of program by the United States military to refer to proposed training and logistics schedules, which were the problems that Dantzig was studying at the time. (Additionally, later on, the use of the term "programming" was apparently important for receiving government funding, as it was associated with high-technology research areas that were considered important.)
Other important mathematicians in the optimization field include:
 Probability
ProbabilityEdited By:
Arip Nurahman
Indonesia University of education
Sources from:
Wikipedia
Probability is the likelihood or chance that something is the case or will happen. Probability theory is used extensively in areas such as statistics, mathematics, science and philosophy to draw conclusions about the likelihood of potential events and the underlying mechanics of complex systems.
 Statistics
StatisticsEdited By:
Arip Nurahman
Indonesia University of education
Sources from:
Wikipedia
Statistics is a mathematical science pertaining to the collection, analysis, interpretation or explanation, and presentation of data. It is applicable to a wide variety of academic disciplines, from the natural and social sciences to the humanities, and to government and business.
Statistical methods can be used to summarize or describe a collection of data; this is called descriptive statistics. In addition, patterns in the data may be modeled in a way that accounts for randomness and uncertainty in the observations, and then used to draw inferences about the process or population being studied; this is called inferential statistics. Both descriptive and inferential statistics comprise applied statistics. There is also a discipline called mathematical statistics, which is concerned with the theoretical basis of the subject.
The word statistics is also the plural of statistic (singular), which refers to the result of applying a statistical algorithm to a set of data, as in economic statistics, crime statistics, etc.
History
-
"Five men, Conring, Achenwall, Süssmilch, Graunt and Petty have been honored by different writers as the founder of statistics." claims one source (Willcox, Walter (1938) The Founder of Statistics. Review of the International Statistical Institute 5(4):321-328.)
Some scholars pinpoint the origin of statistics to 1662, with the publication of "Observations on the Bills of Mortality" by John Graunt. Early applications of statistical thinking revolved around the needs of states to base policy on demographic and economic data. The scope of the discipline of statistics broadened in the early 19th century to include the collection and analysis of data in general. Today, statistics is widely employed in government, business, and the natural and social sciences.
Because of its empirical roots and its applications, statistics is generally considered not to be a subfield of pure mathematics, but rather a distinct branch of applied mathematics. Its mathematical foundations were laid in the 17th century with the development of probability theory by Pascal and Fermat. Probability theory arose from the study of games of chance. The method of least squares was first described by Carl Friedrich Gauss around 1794. The use of modern computers has expedited large-scale statistical computation, and has also made possible new methods that are impractical to perform manually.
Financial mathematics
Edited By:
Arip Nurahman
Indonesia University of education
Sources from:
Wikipedia
Mathematical finance
Mathematical finance is the branch of applied mathematics concerned with the financial markets.
The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive, and extend, the mathematical or numerical models suggested by financial economics. Thus, for example, while a financial economist might study the structural reasons why a company may have a certain share price, a financial mathematician may take the share price as a given, and attempt to use stochastic calculus to obtain the fair value of derivatives of the stock (see: Valuation of options).
In terms of practice, mathematical finance also overlaps heavily with the field of computational finance (also known as financial engineering). Arguably, these are largely synonymous, although the latter focuses on application, while the former focuses on modeling and derivation (see: Quantitative analyst).
The fundamental theorem of arbitrage-free pricing is one of the key theorems in mathematical finance.
Many universities around the world now offer degree and research programs in mathematical finance.
Mathematical finance articles
Mathematical tools
Derivatives pricing
See also
External links

Game theory
Edited By:
Arip Nurahman
Indonesia University of education
Sources from:
Wikipedia
Game theory is a branch of applied mathematics that is used in the social sciences (most notably economics), biology, engineering, political science, computer science (mainly for Artificial Intelligence), and philosophy. Game theory attempts to mathematically capture behavior in strategic situations, in which an individual's success in making choices depends on the choices of others. While initially developed to analyze competitions in which one individual does better at another's expense (zero sum games), it has been expanded to treat a wide class of interactions, which are classified according to several criteria. Today, “game theory is a sort of umbrella or ‘unified field’ theory for the rational side of social science, where ‘social’ is interpreted broadly, to include human as well as non-human players (computers, animals, plants)” (Aumann 1987).
Traditional applications of game theory attempt to find equilibria in these games—sets of strategies in which individuals are unlikely to change their behavior. Many equilibrium concepts have been developed (most famously the Nash equilibrium) in an attempt to capture this idea. These equilibrium concepts are motivated differently depending on the field of application, although they often overlap or coincide. This methodology is not without criticism, and debates continue over the appropriateness of particular equilibrium concepts, the appropriateness of equilibria altogether, and the usefulness of mathematical models more generally.
Although some developments occurred before it, the field of game theory came into being with the 1944 book Theory of Games and Economic Behavior by John von Neumann and Oskar Morgenstern. This theory was developed extensively in the 1950s by many scholars. Game theory was later explicitly applied to biology in the 1970s, although similar developments go back at least as far as the 1930s. Game theory has been widely recognized as an important tool in many fields. Eight game theorists have won Nobel prizes in economics, and John Maynard Smith was awarded the Crafoord Prize for his application of game theory to biology.
Contents
 ,
, 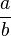 , where b is not
, where b is not  , but it is said to be in simplest form when a and b have no common
, but it is said to be in simplest form when a and b have no common 



 , the length of the diagonal in a unit square.
, the length of the diagonal in a unit square.
 R from some
R from some 
















